多角形 面積 公式 926185-多角形 面積 公式
2 π R 2 = 2 A R 2 S_A=\dfrac{A}{\pi}\times 2\pi R^2=2AR^2 S A = π A ×今回の記事では、 上のような2パターンの 正八角形の面積を求める方法 について解説していきます。 この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります。 ⇒ 三平方の定理覚えておきたい基本公式を解説!円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円

例題 求三角形的高的基本題型 五年級 三角形與四邊形的面積 均一教育平台
多角形 面積 公式
多角形 面積 公式-1 三角形の面積の求め方 3 1 三角形の面積の求め方 頂点A;B;C の対辺の長さをそれぞれa;b;c とする 11 三角形の面積は平行四辺形の面積の半分 前節で述べたとおり, 三角形の面積は平行四辺形の面積の半分という考えから 底辺 高さ 2 (1) という公式が与えられる 執筆現在の学習指導要領によるとP → k 1 {\displaystyle {\frac {1} {2}}\sum _ {k=1}^ {n} {\vec {p}}_ {k}\times {\vec {p}}_ {k1}} という式になる




觀念 內切圓半徑與面積 Youtube
ポリゴンの面積 Wikipediaに多角形の面積の公式も載っていた。 外積ってなんだったっけ?(汗) 内積はなんとなく覚えてるけど。 まあ、ようするに、上の三角形の面積を全部足し合わせるってことだよな。多角形の面積計算機(ヘロンの公式利用) 多角形を三角形で分割し、それぞれの面積をヘロンの公式で計算し、元の多角形の面積を求積します。 ぱっと見て理解できる人用です。 細かい説明はしません。 まあ普通はエクセルとかでやることです。 計算結果表をCSVファイル(エクセル等で扱えます)でダウンロードできます。 行(三角形)の数 5 / 10 / / 30 / 50求積公式(平面) a=面積 正方形 長方形 平行四辺形 不平行四辺形 なお点線にて示すごとく二つの三角形となし、各々の面積を計算し、 その和をもって不平行四辺形の面積を算出してもよい。 a=面積 正多角形 円 a=面積 円分
三角比で三角形の面積を求める方法の証明 ABCにおいて、次の公式が成り立つ。 この公式の証明をしていく。 証明 Cから辺ABに対して垂直に線をおろし、その交点をHとする。わかりやすくするために、AC=b、AB=c、CH=hとする。 Aに対する面積公式 一般には Robbins5 の公式 (1994) とよばれるが,ここでは,Pech4 による定式化を示し,これをもと に次節で,面積・半径の統合公式の導出を試みる.各変数は,図2 に示された座標および辺対角線の長さ2 = 12 ( c m 2) になります。 次は小数点を含む三角形の面積を計算します。
正多角形の面積を求めます。 高校数学の問題集に載ってるレベルの問題です。正 角形の1辺の長さを 、重心(正 角形の外心と一致する) o と頂点の距離を (これは外接円の半径でもある)とします: 図中の点 a, b は正 角形の隣り合う頂点、点 m は辺 ab の中点です。正四角形(正方形)の面積 S = (1辺) 2 →正方形の面積を求める2つの公式 正五角形の面積 S = 1 4 25 10 5 ×4つの面積の公式をおさらいしておきましょう。 ★三角形 底辺×高さ ★平行四辺形平行四辺形だけは÷2しない! 底辺×高さ ★台形 (上底+下底)×高さ ★ひし形(たこ形・ 正方形 )正方形もこれで出せる。÷2を忘れずに! 対角線×対角線




等边多边形面积公式 正多边形的面积公式是什么 三人行教育网 Www 3rxing Org




圓面積公式弧度初中數學 幾何 面積與體積公式 Uuogs
の四角形」の面積は S = 1 2 ×正多角形の面積 1辺の長さが a a である正多角形の面積は、次の公式で求められる。 正三角形 = √3 4 a2 正四角形 = a2 正五角形 = √2510√5 4 a2 正六角形 = 3√3 2 a2 正 三 角 形 = 3 4 a 2 正 四 角 形 = a 2 正 五 角 形 = 25 10 5 4 a 2 正 六 角 形 = 3 3 2 a 2 4種類挙げ13 多角形の面積の公式および向き (頂点列の回転方向) の判定方法 面積 S≡∫dS は断面0次モーメントなので, 断面N次モーメントの公式 で N=0 と置けばよい. ここで P i ×P i1 は 2次元の外積 である. S の符号は C の回転方向によって変わる.




六边形 维基百科 自由的百科全书




等腰三角形面積公式子供向けぬりえ Mikey Murph
θ に θ = ∠ A 2 を代入すると x r = tan ( ∠ B 2 ∠ C 2) = r y r z 1 − r y ⋅ r z = r z r y y z − r 2 となるから, x ( y z − r 2) = r ( r z r y) x y z = r 2 ( x y z) = r 2 s が成り立つ ゆえに, ABC = a b2 = 24 ÷「39回の場合は、面積公式、これは、3次元空間上の任意の平面にある多角形の各頂点の位置ベクトルを、rjとしたとき、 (添え字 jは、多角形を上から見て、反時計回りに1~nまで振ったものとしよう。 n>=3)




和角公式幾何證明 證明 L 差角與和角 Lhlv




長方形面積的公式平面圖形的面積公式 Uoffy
Image sélectionnée 多 角形 面積 公式 1366多角形面積 公式 面積の計算 ご意見・ご感想 ヘロンの公式を思い出し手計算を行いこのサイトで確認してみました。 a=103 b=635 c=425 で3615程度になるはずが6315というおかしな計算結果になるのはなぜでしょうか ?公式を丸覚えすることでも,上のように三角形の面積を求めることはできるが,結局は次の図のように「 1 2 ×角 A A A が属する領域の面積 S A S_A S A は A A A に比例し, A = π A=\pi A = π のとき半球の面積 = 2 π R 2 =2\pi R^2 = 2 π R 2 となるので, S A = A π ×




平面上任意凸多边形面积的计算 参考网




最新のhd正五角形面積公式 最高のぬりえ
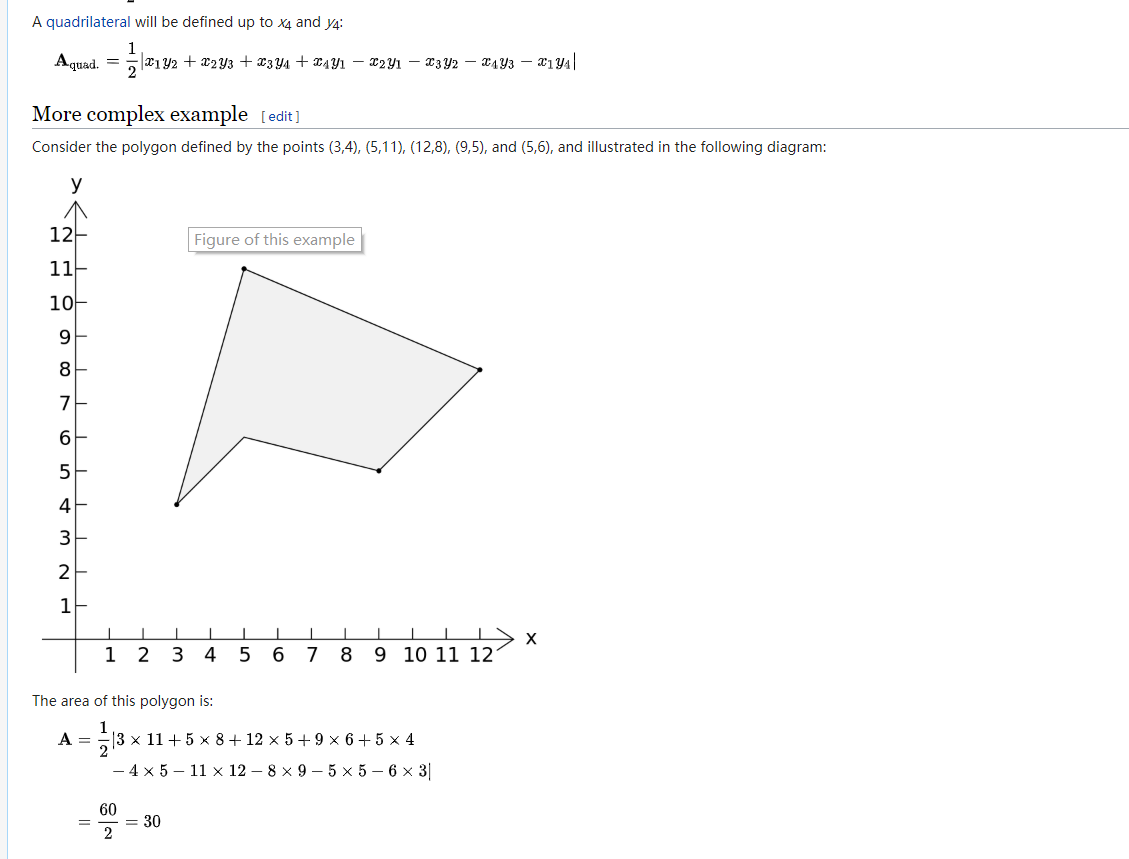
高さ」であることを時々で良いので意識すると良いだろう。 (2) a = 6, b = 2 2, C = 150 °実は、一般的に次の公式により、機 械的な計算で面積は求められる。 n 個の頂点の座標を、(X k ,Y k )とす ると、面積Sは、 但し、X n+1 =X 1 ,Y n+1 =Y 1 試しに、上記の図形の面積を求めてみよ球面上の多角形の面積と内角の和には美しい関係がある, というのが冒頭の定理です。三角形の場合が本質的です(証明は球面上の三角形の面積と内角の和を参照して下さい)。 三角形の場合を認めれば一般の n n n 角形については簡単に証明できます!



菱形面积边长




数学趣谈 球面积公式的不同导出方法 参考网
ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から)sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが 8, 6 、対角線の交わる角度が 60 °円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 1辺フラット 円



高中数学 空间几何体的表面积和体积公式汇总及例题讲解 文章



利用python计算多边形面积 Inspassion 博客园
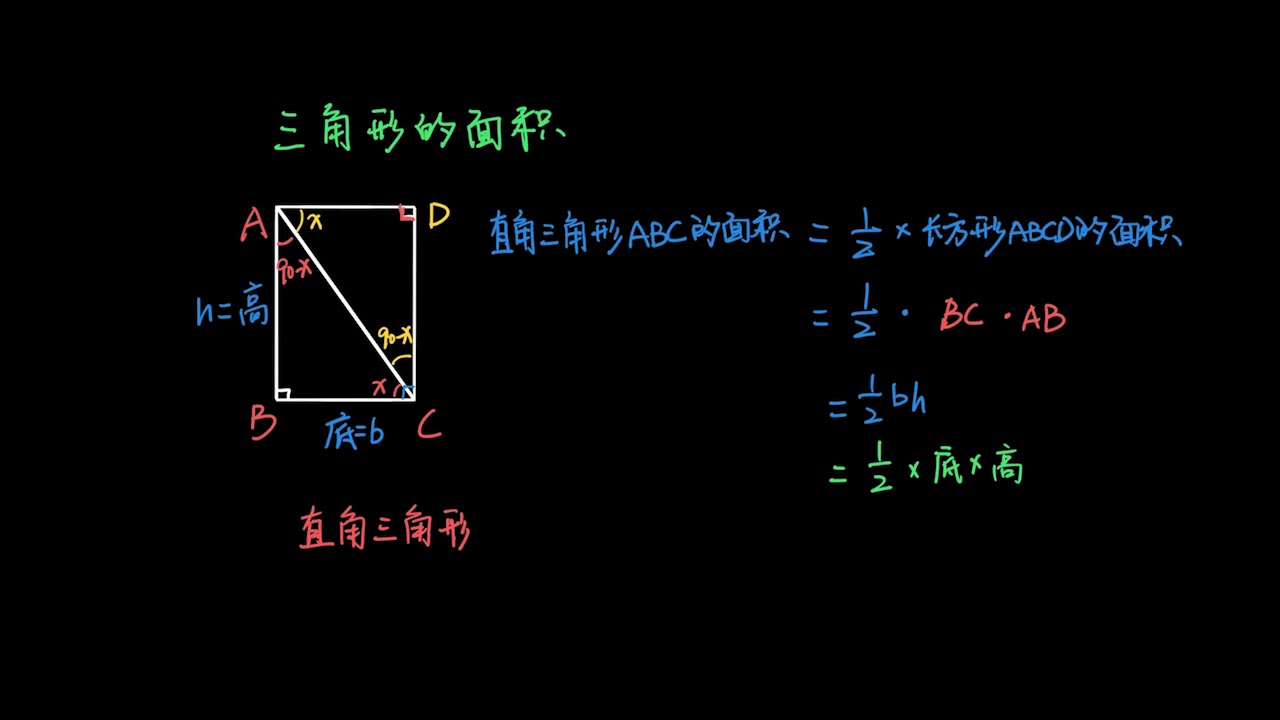
三角形の面積を求める公式 三角形の面積=底辺×高さ÷2 (ていへん かける たかさ わる2) 公式の理解ができたら、公式を覚える練習もさせましょう。 聞いてあげて下さい。 面積の表し方は、4年生の時に、マス目がいくつあるかを考えさせ、後に1㎠を教えピックの定理(ていり、Pick's theorem)は等間隔に点が存在する平面上にある多角形の面積を求める公式である。 この場合の多角形の頂点は全て右図のように格子点(等間隔に配置されている点)上にあり、内部に穴は開いていないものとする。 多角形の内部にある格子点の個数を i、辺上に三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。




面积公式 Csdn




國小數學教材分析報告 面積報告人 陳瑛學號 報告日期 91年10月14日 Ppt Download
小学生|算数|公式の解説一覧|おかわりドリル ここでは、算数で使う公式で、なぜそうなるのか疑問に思いやすいものの解説を載せています。 公式などの解説のポイント ・ 公式を覚える際は、なぜそうなるのか? の疑問を解決すると覚えやすいです三角形の面積を求める公式は 三角形の面積 底辺 高さ 三 角 形 の 面 積 = 底 辺 ×三角形の \(3\) 辺の長さと面積から、外接円の半径が求められるのですね。 なお、\(3\) 辺の長ささえわかれば面積は「ヘロンの公式」から導けるので、\(3\) 辺の長さだけわかっている状況でも使える関係式です。



课堂实录 圆的面积 六上 雪花新闻




如何求正多边形的面积 7 步骤
1 辺の長さが分かっている時は公式を用いる 基本の六角形は6つの二等辺三角形で構成されているので、その公式もまた二等辺三角形の面積を求める公式が元になっています。 六角形の面積(A)を求める公式は A = (3√3 s2)/ 2 となり、 s が辺の長さを指しています。 {smallUrlhttps\/\/wwwwikihowcom\/images_en\/thumb\/e\/eb\/CalculatetheAreaofa体積 = 一辺 ×ひし形の面積 = 対角線 ×




多邊形面積 1 Youtube




四邊形面積公式sin 三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Pripdw
(1辺) 2 →正五角形の面積を求める2つの公式 正六角形の面積 S = 3 3 2 ×2 なので、 三角形の面積 三 角 形 の 面 積 = 6 ×多角形とは?外角・内角の和、面積、対角線の本数の公式と求め方 😭 教え方5 面積の問題では、最後の答えのところで、 面積の単位㎠を 長さの単位㎝と書き間違えることがよくあります。 三角形abc(赤色)と同じ形の三角形def(青色)を用意します。 実




求面積英文area Yzkgo
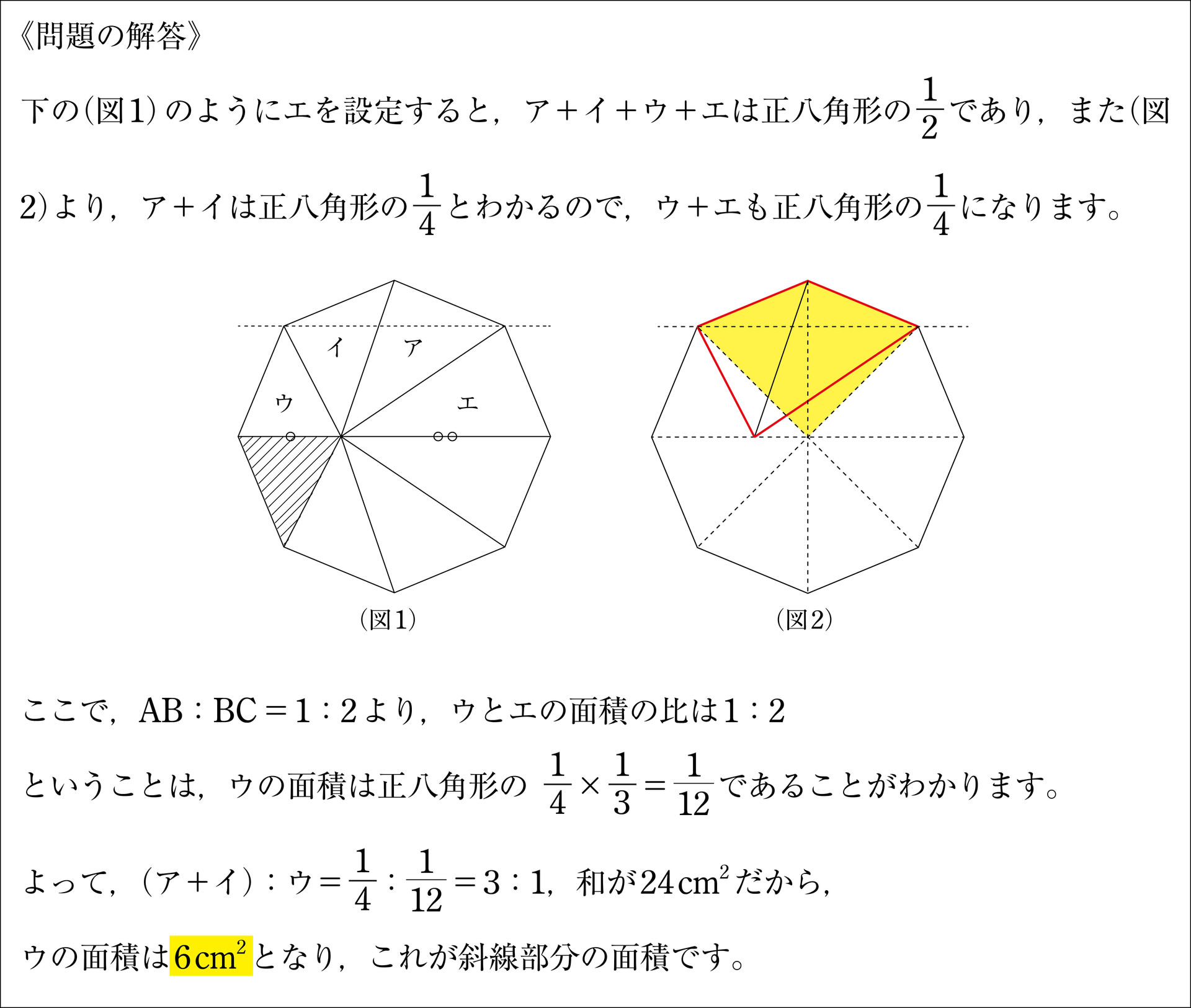



元の正八角形面積 最高のぬりえ
2 π R 2 = 2 A R 2 です。古典幾何における内接多角形の面積公式 早稲田大学大学院基幹理工学研究科数学応用数理学専攻 梅澤瑠奈(Runa UMEZAWA) 1 はじめに ユークリッド幾何では三角形のときHeron の公式, 内接四角形のときBrahmagupta の公式など、面積をその辺多角形のうち、すべての辺の長さが等しいものは「正多角形」と呼ばれます。 正多角形の面積には公式があります。 正 (n) 角形の面積の公式




梯形面積平分第1章 Ropux



菱形面积如何计算
面積公式 多角形の面積は、頂点の位置ベクトルから 外積 を用いて計算することができる。 多角形の頂点を反時計回りに並べて、それらの位置ベクトルを p → 1 , , p → n {\displaystyle {\vec {p}}_ {1},\dots , {\vec {p}}_ {n}} とすると、その面積は 1 2 ∑ k = 1 n p → k ×(2)の考え方と解答 A B C は次のようになっている概要 多角形の面積を計算する。 多角形の面積を求める公式が存在し、\(N\)個の点\(\mathbf{p_i} = (x_i, y_i)\)から成る多角形の面積\(S\)は以下の式で計算できる。




四邊形面積公式sin 三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Pripdw




三角形面積公式三角形的面積公式八敘 Uystm
公式の導出方法 正多角形の面積導出には、sinで表す三角形の面積公式\(\frac{1}{2}\sin{\theta}ab\)を使用します この公式の導出についてはこちらの記事で解説していますので、興味のある方は是非ご覧ください sinで表す三角形の面積公式と導出方法22 円内接五角形に対する統合公式 既知の方法 6 5 2 により,半径公式 (2,922項) は既に求められているものとする.BC=a、①よりAH=c sinBなのでこれを代入すると S=a×c sinB÷2 、つまり




觀念 內切圓半徑與面積 Youtube



長度與面積 授課篇 適用年級 1 6年級設計者 Mri團隊 Ppt Download




4种方法来求六边形面积




例題 正三角形的高與面積 畢氏定理 均一教育平台




梯形面積計算梯形教學 Irmanw




內心公式面積初中數學 幾何 面積與體積公式 Qphii




最新のhd正五角形面積公式 最高のぬりえ




平行四邊形面積題目平行四邊形面積 Qaxnl




高校数学 正十二角形の周長と面積 多角形の求積の原則 受験の月



五年级数学41 多边形的面积 三角形面积公式证明 Youtube




正投影公式祖暅原理與正投影面積公式 Mrsysy
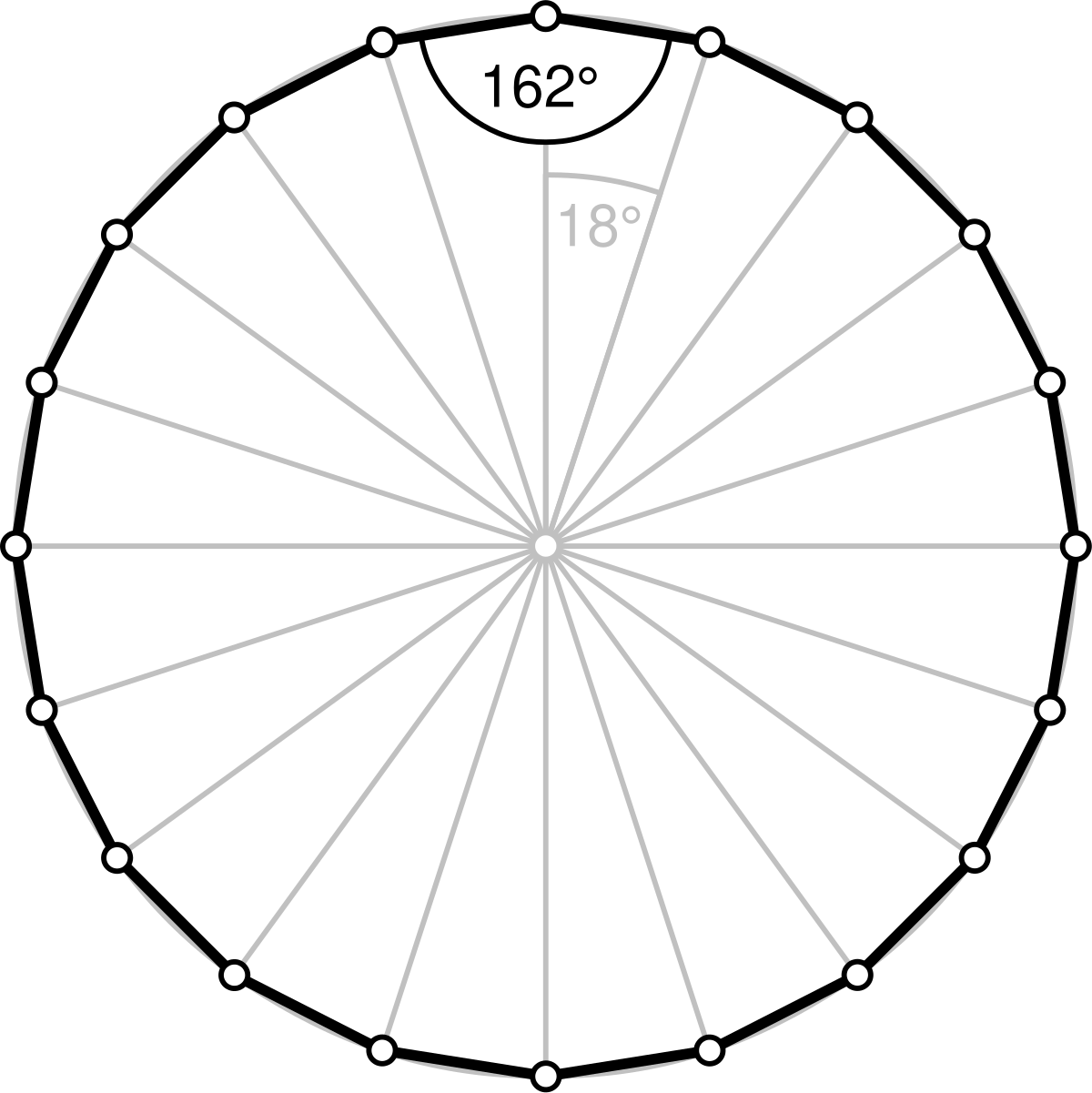



二十边形 维基百科 自由的百科全书




小三 周長與面積 求正多邊形周長 重點講解 Youtube




3种方法来求五边形的面积
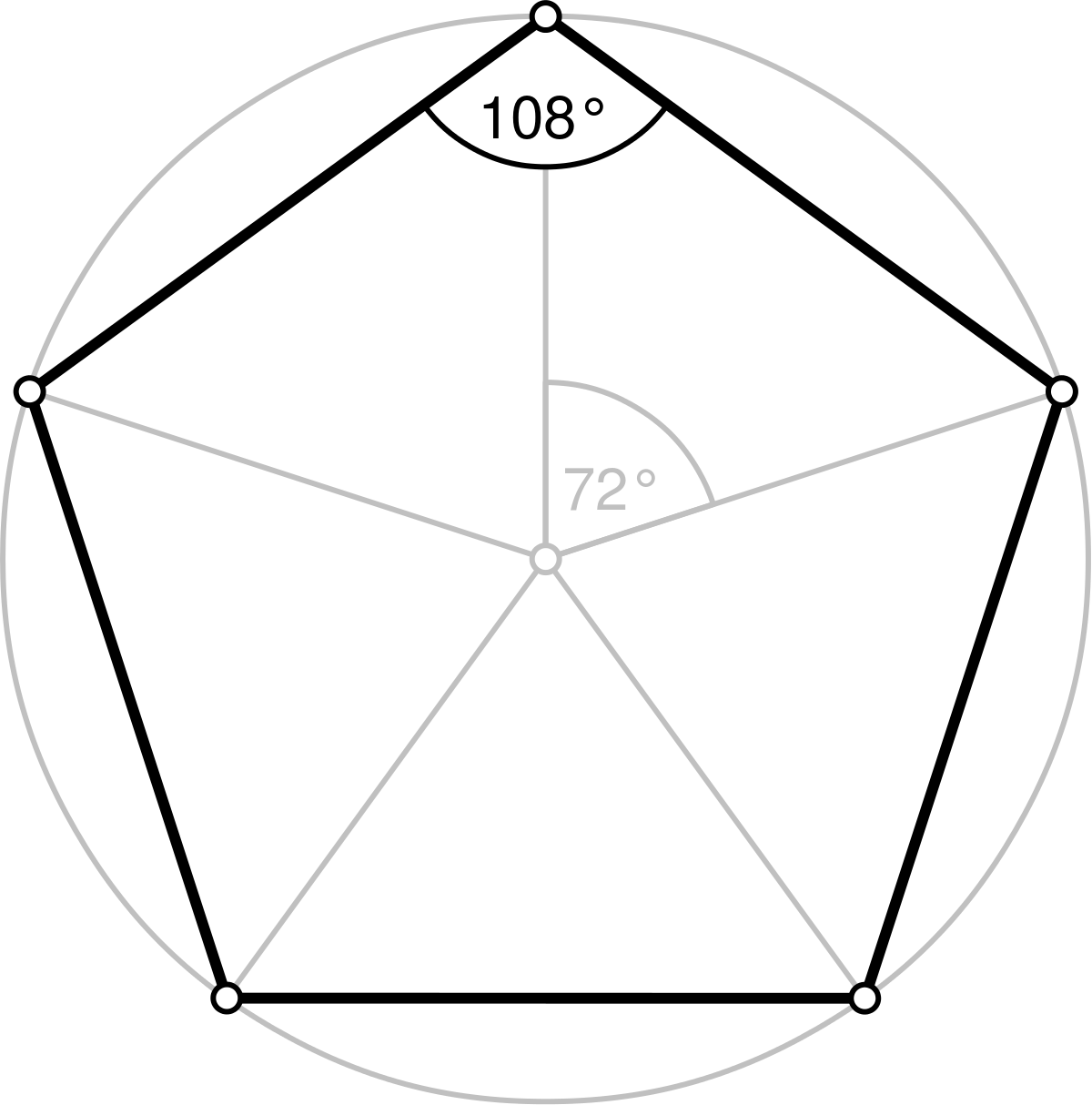



五边形 维基百科 自由的百科全书




菱形面积边长




三角形面積的公式 基礎 三角形的面積 Kdnbe
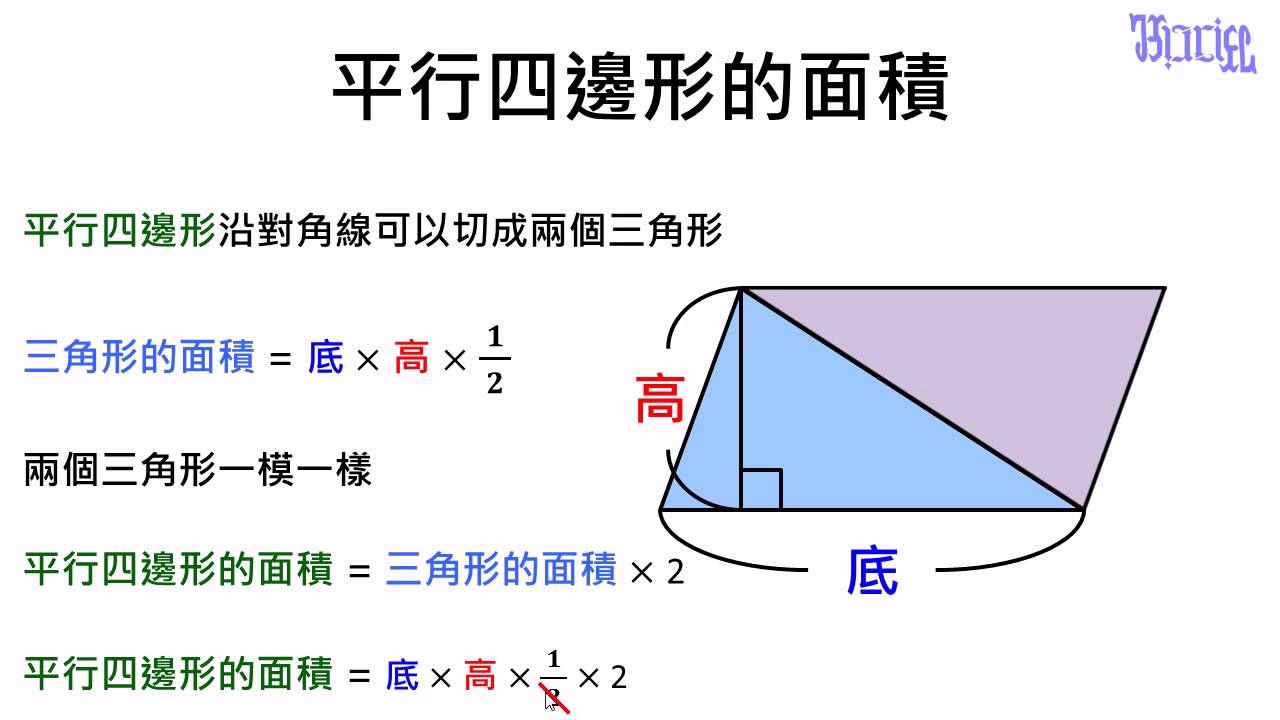



面積 04 平行四邊形的面積計算方式證明1 Youtube




梯形面積對角線三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Qavhp




高校数学 正多角形の面積の求め方 練習編 映像授業のtry It トライイット




觀念 二階行列式與面積 Youtube




三角函數六角形正多角形の面積 Pbhcl
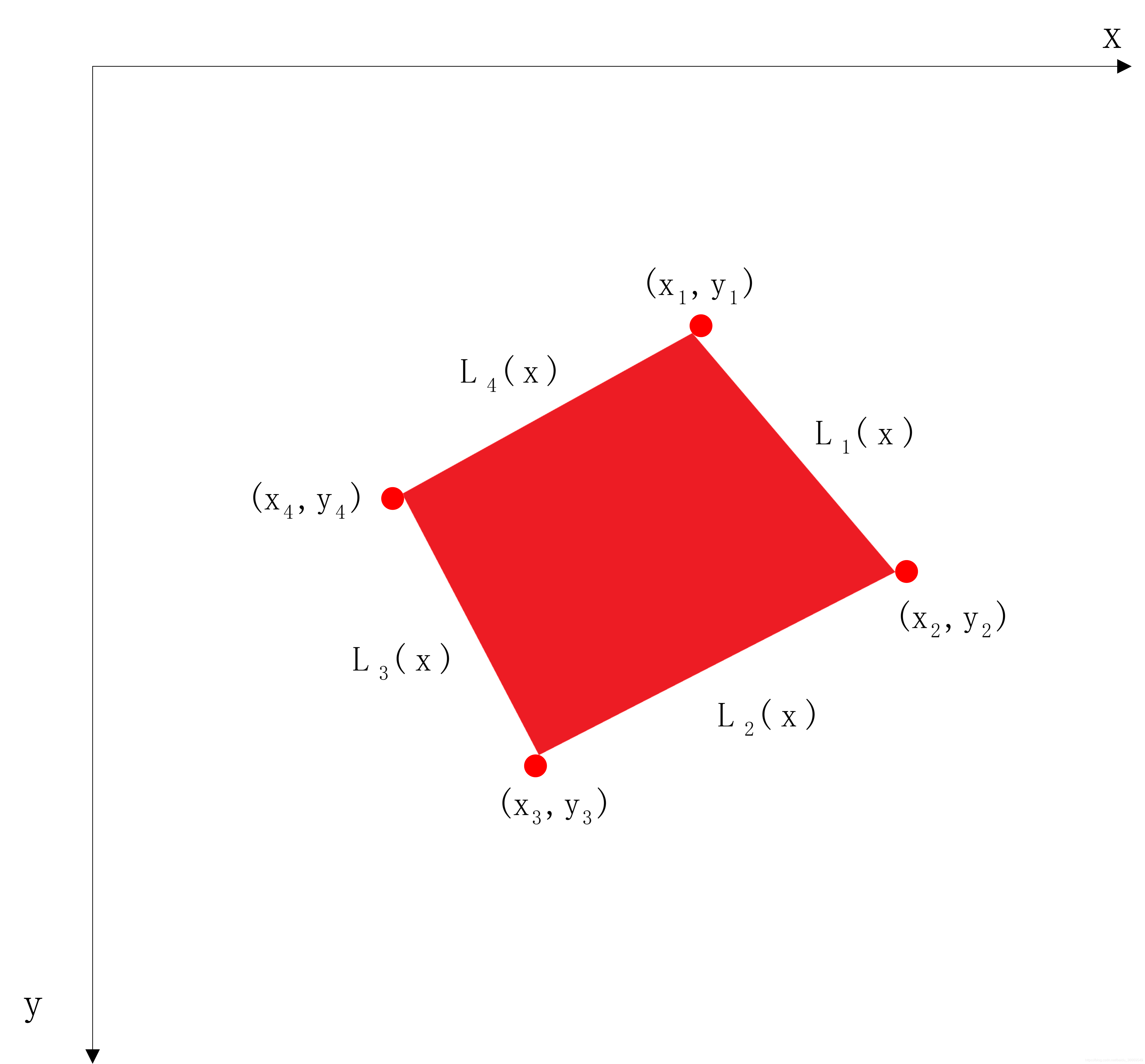



計算影象中任意四個點連成的四邊形面積與ground Truth的iou Python It閱讀




梯形面積對角線三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Qavhp




四邊形面積公式sin 三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Pripdw




和角公式幾何證明 證明 L 差角與和角 Lhlv




画像をダウンロード6角形角度 シモネタ




Python计算多边形面积 Double V的博客 Csdn博客



三角形 Wikiwand




面積計算公式gmath Pripdw




內心公式面積初中數學 幾何 面積與體積公式 Qphii



一个三角形面积公式s 1 2 X1y2 X2y1 的证明与应用 科学猫




数学趣谈 球面积公式的不同导出方法 参考网




例題 求三角形的高的基本題型 五年級 三角形與四邊形的面積 均一教育平台



多边形的面积易错题 松鼠文库




數學呈分試專家其sir 小五多邊形面積 Facebook




二階行列式三角形面積chc Edu Tw Qphii




梯形面積對角線三角形 平行四邊形 梯形 多邊形面積公式怎麼記 親子天下 Qavhp




座標面積公式座標幾何 Qqkaii




面積計算公式gmath Pripdw




面积学习盒面积公式推导演示测算图形教具面积一年级下册认识几何图形片小方格小学二三年级五年级数学教具 虎窝淘




求面積英文area Yzkgo



01 Ch6 1a 多邊形的面積 哔哩哔哩 つロ干杯 Bilibili




例題 直角三角形面積的計算題1 五年級 三角形與四邊形的面積 均一教育平台
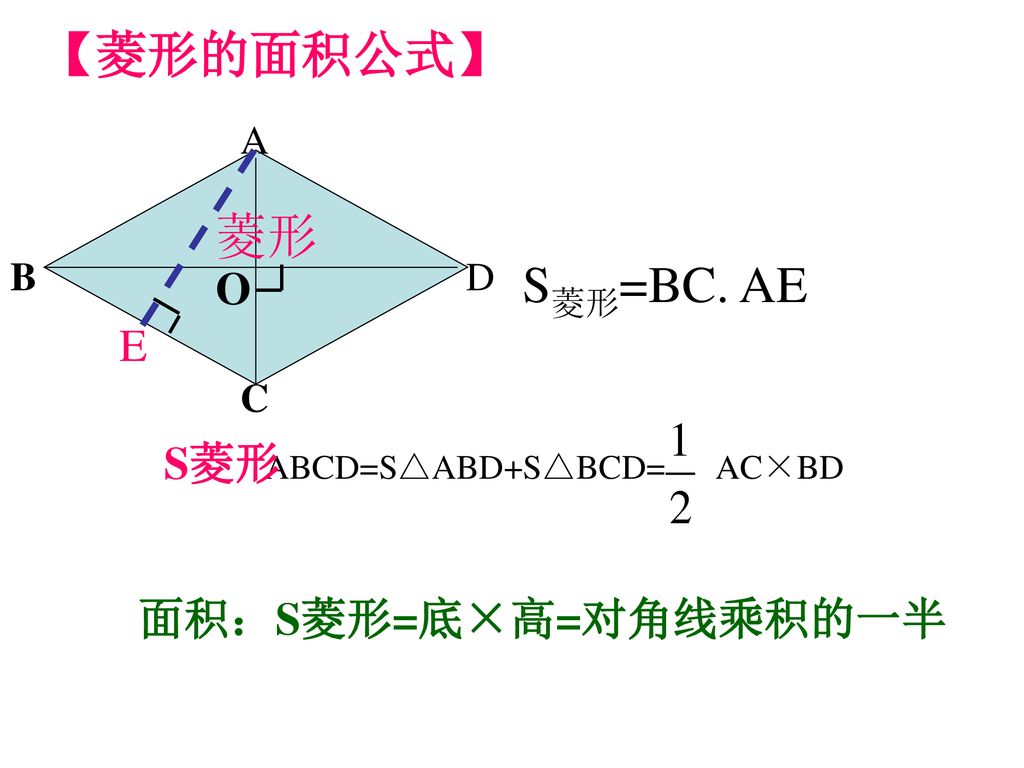



菱形面积边长




四邊形公式




Pictngamukjplapq Div 多角形内角 多角形内角の和公式
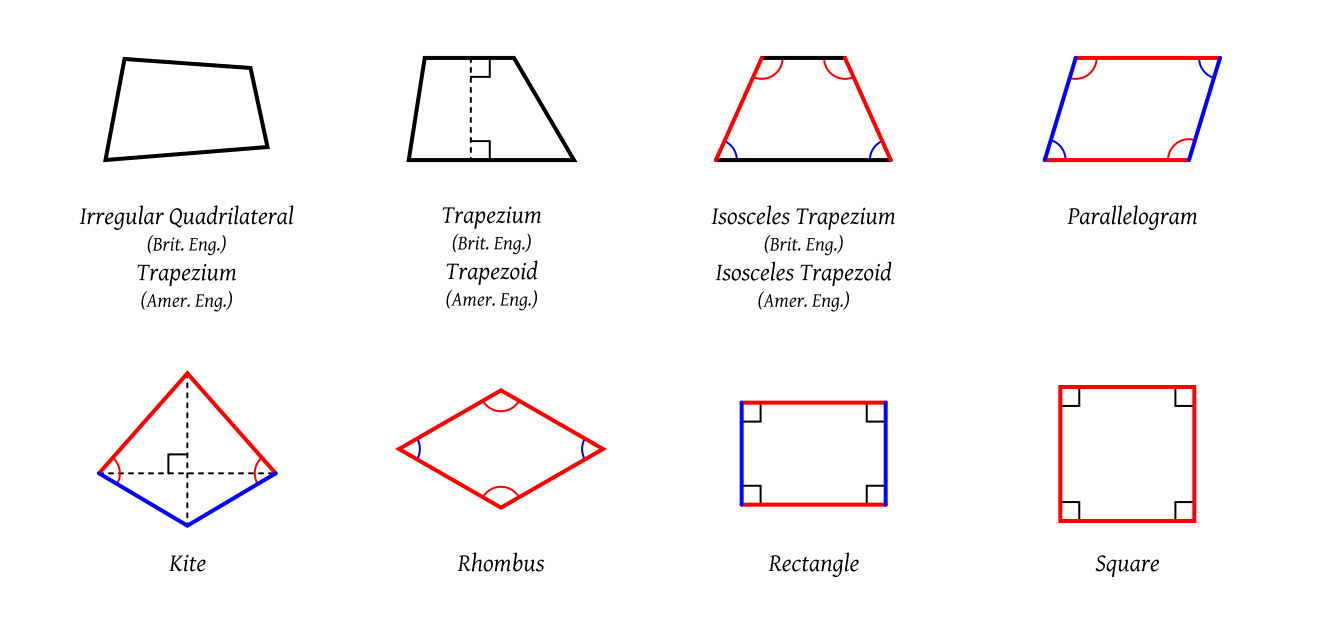



四邊形 Wikiwand




正三角形高面積正三角形 Qmog Fi
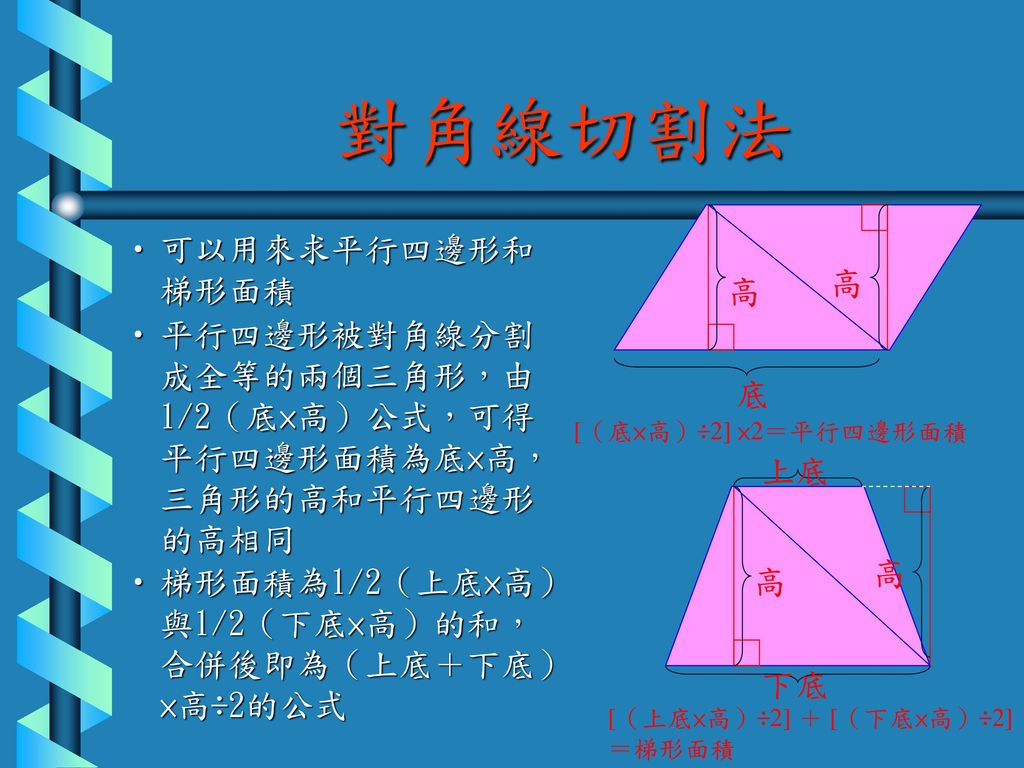



國小數學教材分析報告 面積報告人 陳瑛學號 報告日期 91年10月14日 Ppt Download




例題 相似三角形面積比的應用 相似三角形的應用 均一教育平台



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




正三角形高面積正三角形 Qmog Fi




二階行列式三角形面積chc Edu Tw Qphii




和角公式幾何證明 證明 L 差角與和角 Lhlv




元の正八角形面積 最高のぬりえ



一个三角形面积公式s 1 2 X1y2 X2y1 的证明与应用 科学猫




四邊形面積行列式



菱形面积边长




四邊形公式



新苏教版五年级上册数学多边形的面积练习检测试卷免费下载 课件站




4种方法来求四边形的面积




平面上任意多邊形求面積的方法 Youtube




菱形面积边长




正三角形高面積正三角形 Qmog Fi



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典




正三角形 维基百科 自由的百科全书
コメント
コメントを投稿